Implied Volatility
This tutorial written and reproduced with permission from Peter Ponzo
Historical Volatility (HV) is calculated by looking at historical returns and calculating some kind of average deviation from their mean value using the magic formula for Standard Deviation … also called Volatility.
But aren’t their several magic formulas for Standard Deviation?
However, I’m not interested in the particular formula one uses for Standard Deviation, I’m interested in the relationship between HV (calculated via one of them thar formulas), and Implied Volatility (IV).
Huh?
Remember the Black-Scholes formula for calculating the “fair” price of a call option?
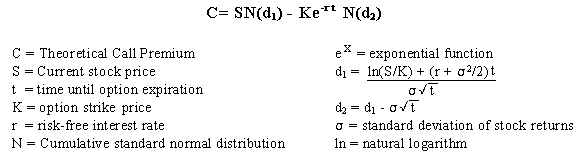
That guy labelled σ is the number one inserts to represent the stock’s volatility. Alas, if one uses HV, it rarely gives the actual price at which the option is selling.
How come?
Well, I guess that HV is a value generated from past returns and perhaps people who buy options are interested in future returns, future volatility, future option prices, and the value they place on an option reflects their opinion of future values and …
So what volatility should one use, in that Black-Scholes formula?
Well, the value of σ which gives the actual option price is called …
Don’t tell me! It’s Implied Volatility, right?
Yes, it’s IV.
So how do they compare … HV and IV?
That’s what I asked myself … hence this tutorial.
So what if using HV in Black-Scholes gives a larger option premium?
Larger than it’s currently selling for? That’d means that the IV, which gives the actual selling price, is smaller … so I guess investors think the option will go down. Anyway, let’s play with that …
Calculating Implied Volatility
Our problem is to calculate IV (from the Black-Scholes formula) in terms of the other parameters, namely C, S, K, r, and T .
Good luck!
I don’t think I can do that, but let’s give it a try. First some notation:
Define A = C/S,
B = K/S,
R = rT and
let y = σ SQRT(T) = IV SQRT(T).
The Black-Scholes formula then looks like:
[1] A = N(d1) – B e-R N(d2)
where
d1 = [ -log(B) + R + (1/2)y2 ] / y
and
d2 = d1 – y
Our problem is to find y in terms of A, B and R.
We rewrite [1] like so:
[2] Error = N(d1) – B e-R N(d2) – A
If, for a given set of numbers A, B and R, a y-value makes Error = 0, then IV = y / SQRT(T).
Yeah, so?
Suppose the relevant values are:
Stock Price: S = $10.00
Strike Price: K = $9.80
Time to expiry: T = 0.25 years
Risk-free rate: r = 4%
Actual call option premium: C = $1.00
Then, plotting the Error versus y gives Figure 1. Then Error = 0 when y = 0.215 or 21.5%
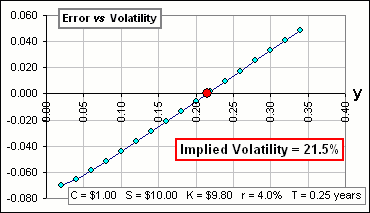
Figure 1
So, what’s your point?
I thought it’d be interesting (now that we have a method for calculating both) to compare IV and HV and, in particular, to determine which of the various definitions of Historical Volatility is closest to Implied Volatility.
Implied Volatility versus Historical Volatility
Okay, we’ll use a spreadsheet where do the following:
Type in some stock symbol and click a button to download a year’s worth of daily stock prices.
Calculate the Standard Deviations (hence Historical Volatiliies) from the downloaded prices. Using Annualized Volatility = (Daily Volatility)*SQRT(250)
– Look up a call option for that stock … one that expires in a few months.
– Identify C, S, K and T … and assume some Risk-free Rate r.
– Calculate the parameters A, B and R as indicated above.
– Find the Implied Volatility and compare to the Historical Volatility.
Then look at …
Why not show the spreadsheet?
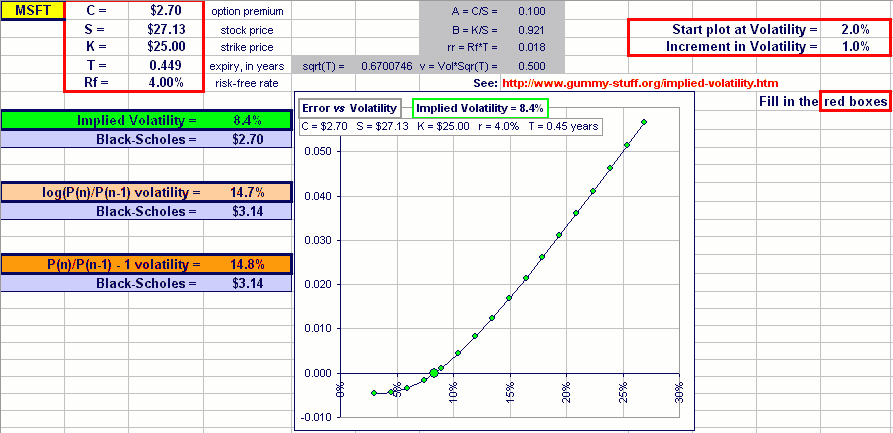
Okay, here’s an example for a MSFT call option:
Click on the picture to download the spreadsheet
Not too close, I’d say.
Well, of course, we might calculate “Annualized Volatility” differently, or use three month’s worth of daily prices (instead of a year’s worth) or …
So, do it.
… we might take another option, maybe one that has a strike price just above the stock price (rather than just below) and …
So, do it.
Okay, here’s a picture:
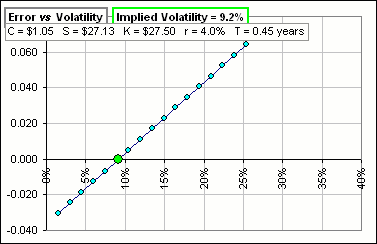
Note that the IV just went up. We could (and many do) take some average of several IV-values for strike prices near the stock price. I’d like to point out another interesting thing:
Consider an “in-the-money” option (meaning K < S). Look again at the B-S equation, namely:
[3] C = S N(d1) – K e-rT N(d2)
If we let y 0 (meaning volatility 0), then d2 d1 +infinity (for S / K > 0) and N(d1) and N(d2) both 1 and …
So C = S – K e-rT, right?
Yes, in the limit as the volatility becomes 0. The interesting point here is that, if S – K e-rT > 0, then the Error > 0 and the plot of Error vs Volatility curve looks like this:
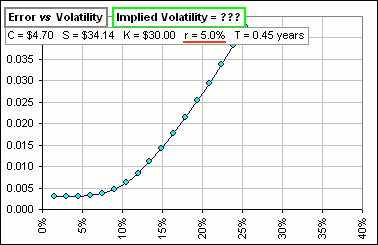
No implied volatility?
Well, it’s clear that the option premium C will be larger than S – K, but will it be larger than S – K e-rT? If not, then there is NO Implied Volatility that’ll give the current option price.
Does that ever happen?
Yeah, but it depends upon what Risk-free Rate you use. If we change that rate from 5% to 3%, we’d get this guy:
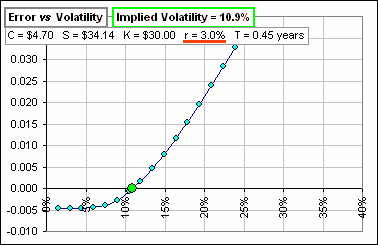
So ya gotta be careful about your assumed risk-free, right?
Yes, in this example you’d need r less than 4% to get an implied volatility.
Is that an invention or a real stock?
Today is Aug 9, 2005. The call expires Jan 20, 2006. The stock is GE.