Statistical Distribution
This tutorial written and reproduced with permission from Peter Ponzo
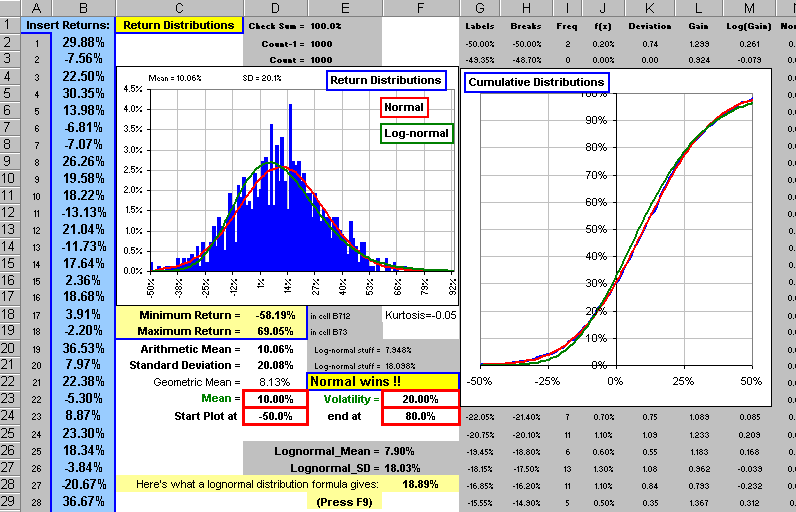
You stare raptly at a collection of stock returns and ask:
Are they distributed Normally or maybe Lognormally or may something else?
Or, you’ve found some strange formula which generates random returns and you ask:
Are they distributed Normally or maybe Lognormally or may something else?
If these question(s) keep you awake at night, maybe this spreadsheet will put you to sleep …
Just RIGHT-click on the picture and Save Target to download a .ZIP’d file. P.S. The spreadsheet may change from time to time … without notice .
On the “Explain” sheet is the formula:
=Mean + Volatility * SQRT(-2 * LN(RAND()))*COS(2*PI() *RAND())
for generating Normally distributed random numbers. That’s the Box-Muller transformation which goes like so: If X and Y are two uniformly distributed, independent random variables lying between 0 and 1, then:
R = SQRT(-2 * lnX) cos(2p*Y)
is normally distributed with Mean = 0 and Standard Deviation = 1. Hence
R = M + V * SQRT(-2 * lnX) cos(2p*Y)
is Normally distributed with Mean = M and Standard Deviation V. Nice, eh?
P.S. R = SQRT(-2 * lnX) sin(2p*Y) is good, too
Since generating the original spreadsheet displayed above … it’s changed